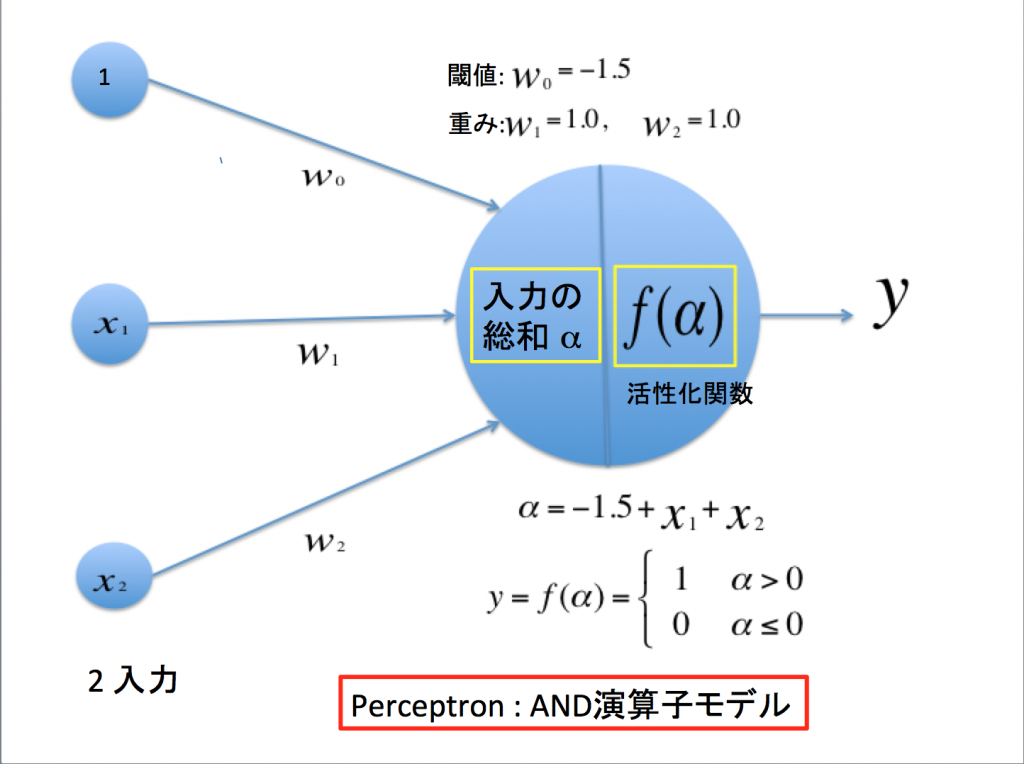
Fig.1 閾値ありのAND演算をするパーセプトロンを実現するPython関数の定義例

①# AND演算に閾値(バイアス項) w0 = -1.5を追加する場合:

閾値w0, 第1層のneutronへの重みw1, w2はAND演算を満足する任意の値に取ってある。

import numpy as np # numpyのインポート

# パーセプトロンでAND演算を実現する
def AND(x1, x2):
x1_x2 = np.array([x1, x2])
w0 = -1.5 # バイアス
w1_w2 = np.array([1.0, 1.0]) # w1、w2の配列
val = w0 + np.sum(w1_w2*x1_x2) # val = w0 + w1・x1 + w2・x2
if val <= 0:
return 0
elif val > 0:
return 1

# 実行ブロック
print(AND(0, 0)) –>　0
print(AND(1, 0)) –>　0
print(AND(0, 1)) –>　0
print(AND(1, 1))  –>　1

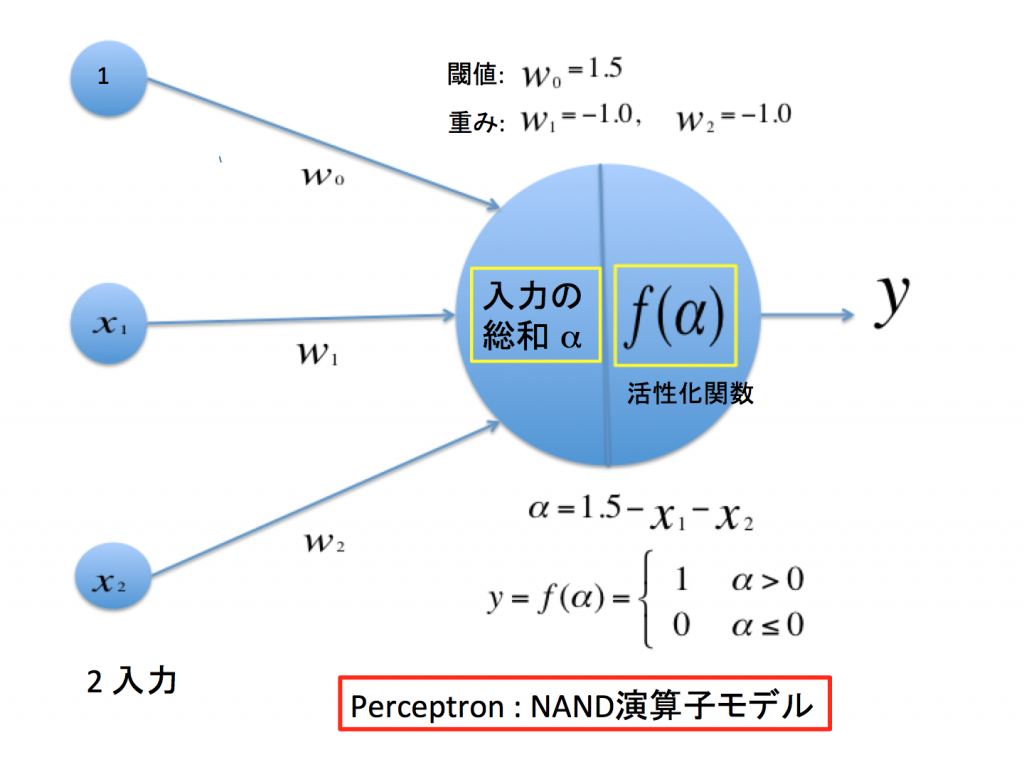
Fig.2 NAND演算をするパーセプトロンを実現するPython関数例

②# NAND演算に閾値(バイアス項)w0 = 1.5を追加する場合:

閾値w0, 第1層のneutronへの重みw1, w2はNAND演算を満足する任意の値に取ってある。

import numpy as np # numpyのインポート

# パーセプトロンでNAND演算を実現する
def NAND(x1, x2):
x1_x2 = np.array([x1, x2])
w0 = 1.0 # バイアス
w1_w2 = np.array([-1.0, -1.0]) # w1、w2の配列
val = w0 + np.sum(w1_w2*x1_x2) # w0 + w1・x1 + w2・x2
if val <= 0:
return 0
elif val > 0:
return 1

# 実行ブロック
print(NAND(0, 0))   –>   1
print(NAND(1, 0))   –>　1
print(NAND(0, 1))   –>　1
print(NAND(1, 1))    –>　0

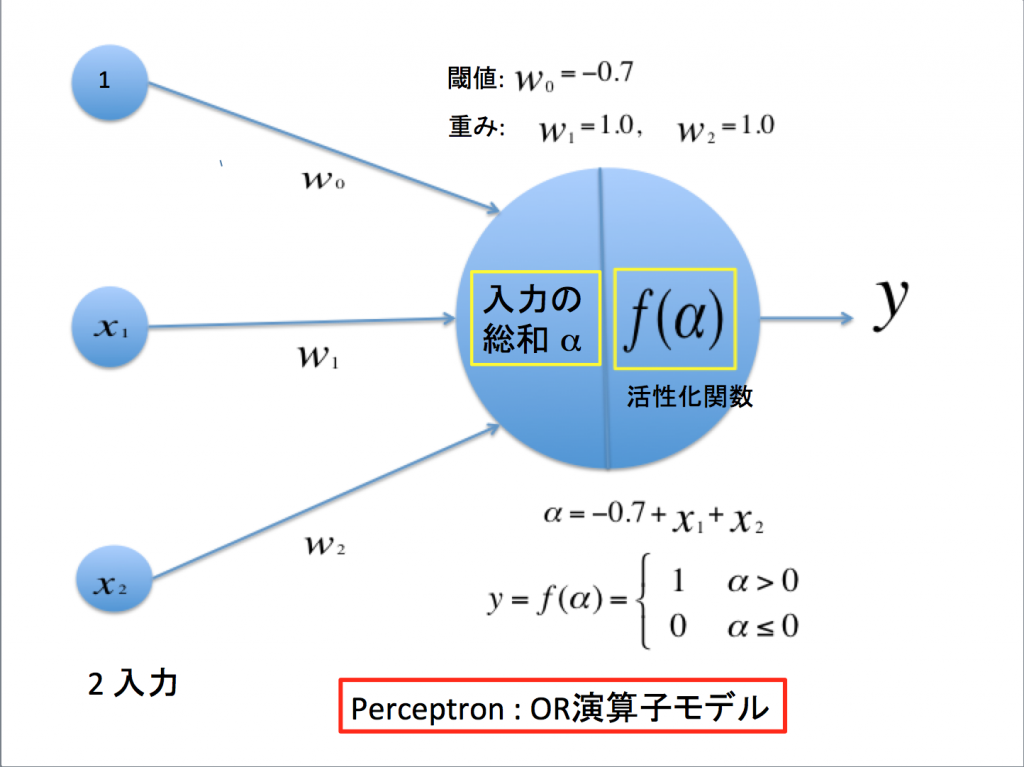
Fig.3 OR演算をするパーセプトロンを実現するPython関数例

③# OR演算に閾値(バイアス項)w0 = -0.7を追加する場合:

閾値w0, 第1層のneutronへの重みw1, w2はOR演算を満足する任意の値に取ってある。

import numpy as np # numpyのインポート

# パーセプトロンでOR演算を実現する
def OR(x1, x2):
x1_x2 = np.array([x1, x2])
w0 = -0.4 # バイアス
w1_w2 = np.array([1.0, 1.0]) # w1、w2の配列
val = w0 + np.sum(w1_w2*x1_x2) # w0 + w1・x1 + w2・x2
if val <= 0:
return 0
elif val > 0:
return 1

# 実行ブロック
print(OR(0, 0))  –>　0
print(OR(1, 0))   –>　1
print(OR(0, 1))    –>　1
print(OR(1, 1))     –>　1

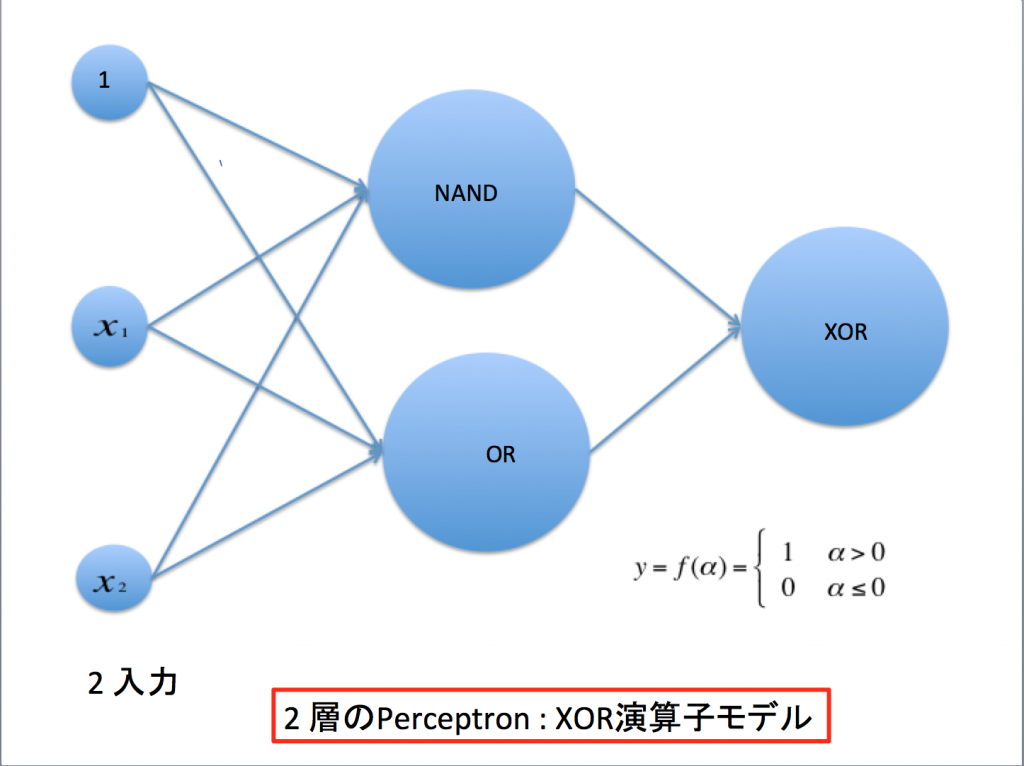
Fig.4 XOR演算をする2層のパーセプトロンを実現するPython関数例

④# 2層のパーセプトロンでXOR演算を実現

まず、第一層のNAND演算と一層のOR演算を実施し、次に第二層で両者のAND演算を実施することによりXOR演算を実現できる。

import numpy as np # numpyのインポート

# ANDパーセプトロン
def AND(x1, x2):
x1_x2 = np.array([x1, x2])
w0 = -1.5 # バイアス
w1_w2 = np.array([1.0, 1.0]) # w1、w2の配列
val = w0 + np.sum(w1_w2*x1_x2) # w0 + w1・x1 + w2・x2
if val <= 0:
return 0
elif val > 0:
return 1

# NANDパーセプトロン
def NAND(x1, x2):
x1_x2 = np.array([x1, x2])
w0 = 1.5 # バイアス
w1_w2 = np.array([-1.0, -1.0]) # w1、w2の配列
val = w0 + np.sum(w1_w2*x1_x2) # w0 + w1・x1 + w2・x2
if val <= 0:
return 0
elif val > 0:
return 1

# ORパーセプトロン
def OR(x1, x2):
x1_x2 = np.array([x1, x2])
w0 = -0.7 # バイアス
w1_w2 = np.array([1.0, 1.0]) # w1、w2の配列
val = w0 + np.sum(w1_w2*x1_x2) # w0 + w1・x1 + w2・x2
if val <= 0:
return 0
elif val > 0:
return 1

# 2層パーセプトロン
def XOR(x1, x2):
_nand = NAND(x1, x2)
_or = OR(x1, x2)
_xor = AND(_nand, _or)
return _xor

# 実行ブロック ################
print(XOR(0, 0))   –>　0
print(XOR(1, 0))    –>　1
print(XOR(0, 1))    –>　1
print(XOR(1, 1))     –>　0

この様に層を重ねたパーセプトロンを多層パーセプトロンと呼ぶ。XOR演算は一層のパーセプトロンでは実現できない。しかし、二層のパーセプトロンにすることでXOR演算が可能となった。パーセプトロンは単層では実現不能な処理であっても多層にすることで実現可能になる。言い換えると、多層のパーセプトロンは非線形で複雑な問題も実現できることが分かる。

参考文献:

夢見るディープラーニング: ニューラルネットワーク[Python実装]入門,

第2章、金城悛哉、秀和システム、2018.