新着情報
プーリング層とドロップアウト層によるCNNの多層化
畳み込みニューラルネットワーク(CNN)の性能向上のため、プーリング手法やドロップアウト手法が考案されている。ここではプーリング層やドロップアウト層を挿入してCNNの多層化による、分類精度の向上について述べる。
(1)最大プーリング手法:プーリング手法の中で最もシンブルで最も効率的な最大プーリング手法について説明する。
例えば、[6×6]の画像に[2×2]の領域を決め、その領域の最大値を出力とするプーリング画像を作成する。この結果出力されるプーリング画像のサイズは[3×3]と入力画像の4分の1になる。
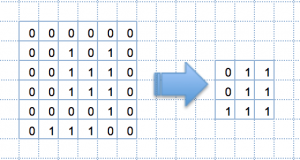
Fig.1. 最大プーリングの実施
プーリングは入力画像の局所的な歪みやズレによる影響を受けにくく、出力される画像サイズは4分の1になるメリットがある。
(2)ドロップアウト手法:
訓練データの学習過程において、個々の訓練データに極端にフィットする過剰適合(Over-fitting)を避けるために実施する。
訓練データ増やさずにOver-fittingを防ぐ、シンプルで効果のある方法である。
ここでは、畳み込みネットワーク(CNN)にプーリング層とドロップアウト層を追加し、7層で構成される深層学習CNNを構築する。
具体的には、第1層と第2層を畳み込み層とし、第3層をプーリング層とし、第4層を再び畳み込み層とし、第5層にプーリング層を配置し、
そう後ろに50%のドロップアウト層とベクトル化するためのFlatten層を挟んで128個のニューロンからなる全結合層を第6層とする。最後に第7層として出力層を配置するが、第6層と第7層の間に25%のドロップアウト層を挟む。
構築された畳み込みニューラルネットワーク(CNN)の構成を以下に図示す。
# プーリング、ドロップアウトを備えた深層畳み込みニューラルネットワーク
import numpy as np
np.random.seed(1)
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.optimizers import Adam
model = Sequential() # Sequentialオブジェクトの生成
# (第1層)畳み込み層
model.add(Conv2D(filters=16, # フィルターの数は16
kernel_size=(3, 3), # 3×3のフィルターを使用
input_shape=(28, 28, 1), # 入力データのサイズ
padding='same', # ゼロパディングを行う
activation='relu' # 活性化関数はReLU
))
# (第2層)畳み込み層
model.add(Conv2D(filters=32, # フィルターの数は32
kernel_size=(3, 3), # 3×3のフィルターを使用
padding='same', # ゼロパディングを行う
activation='relu' # 活性化関数はReLU
))
# (第3層)プーリング層
model.add(
MaxPooling2D(pool_size=(2, 2))) # 縮小対象の領域は2×2
# (第4層)畳み込み層
model.add(Conv2D(filters=64, # フィルターの数は64
kernel_size=(3, 3), # 3×3のフィルターを使用
padding='same', # ゼロパディングを行う
activation='relu' # 活性化関数はReLU
))# (第5層)プーリング層
model.add(
MaxPooling2D(pool_size=(2, 2))) # 縮小対象の領域は2×2
# ドロップアウト層
model.add(Dropout(0.5)) # ドロップアウトは50%
# 出力層への入力を4次元配列から2次元に変換する
model.add(Flatten())
# (第6層)全結合層
model.add(Dense(128, # ニューロン数は128
activation='relu' # 活性化関数はReLU
))
#model.add(Dropout(0.25)) # ドロップアウトは25%
# (第7層)出力層
model.add(Dense(10, # 出力層のニューロン数は10
activation='softmax' # 活性化関数はsoftmax
))
# Sequentialオブジェクトのコンパイル
model.compile(
loss='categorical_crossentropy', # 損失の基準は交差エントロピー誤差
optimizer=Adam(), # 学習方法をAdamにする
metrics=['accuracy'] # 学習評価として正解率を指定
)
model.summary()
により、構築したCNNの概要は以下の様になる。
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 28, 28, 16) 160
_________________________________________________________________
conv2d_2 (Conv2D) (None, 28, 28, 32) 4640
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 14, 14, 32) 0
_________________________________________________________________
conv2d_3 (Conv2D) (None, 14, 14, 64) 18496
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 7, 7, 64) 0
_________________________________________________________________
dropout_1 (Dropout) (None, 7, 7, 64) 0
_________________________________________________________________
flatten_1 (Flatten) (None, 3136) 0
_________________________________________________________________
dense_1 (Dense) (None, 128) 401536
_________________________________________________________________
dense_2 (Dense) (None, 10) 1290
=================================================================
Total params: 426,122
Trainable params: 426,122
Non-trainable params: 0
_________________________________________________________________
訓練データとテストデータの読み込みと加工を以下により実施し、
import numpy as np
# keras.utilsからnp_utilsをインポート
from keras.utils import np_utils
# MNISTデータセットをインポート
from keras.datasets import mnist
# MNISTデータセットの読み込み
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 訓練データ
# 60000x28x28の3次元配列を60000×28x28x1の4次元配列に変換
x_train = x_train.reshape(60000, 28, 28, 1)
# 訓練データをfloat32(浮動小数点数)型に変換
x_train = x_train.astype('float32')
# データを255で割って0から1.0の範囲に変換
x_train = x_train / 255
# 正解ラベルの数
correct = 10
# 正解ラベルを1-of-K符号化法で変換
y_train = np_utils.to_categorical(y_train, correct)
# テストデータ
# 10000x28x28の3次元配列を10000×28x28x1の4次元配列に変換
x_test = x_test.reshape(10000, 28, 28, 1)
# テストデータをfloat32(浮動小数点数)型に変換
x_test = x_test.astype('float32')
# データを255で割って0から1.0の範囲に変換
x_test = x_test / 255
# 正解ラベルを1-of-K符号化法で変換
y_test = np_utils.to_categorical(y_test, correct)
ミニバッジの数を100とし、学習の繰り返し数をepoch=20回として下記のプログラムを実行した。
import time
# 学習を行って結果を出力
start = time.time() # プログラムの開始時刻を取得
history = model.fit(x_train, # 訓練データ
y_train, # 正解ラベル
batch_size=100, # 勾配計算に用いるミニバッチの数
epochs=20, # 学習を繰り返す回数
verbose=1, # 学習の進捗状況を出力する
validation_data=(
x_test, y_test # テストデータの指定
))
# テストデータを使って学習を評価するデータを取得
score = model.evaluate(x_test, y_test, verbose=0)
# テストデータの誤り率を出力
print('Test loss:', score[0])
# テストデータの正解率を出力
print('Test accuracy:', score[1])
# 処理にかかった時間を出力
print("Computation time:{0:.3f} sec".format(time.time() - start))
誤り率と正解率計算の実行結果を以下に示す。
Train on 60000 samples, validate on 10000 samples
Epoch 1/20
60000/60000 [==============================] – 74s 1ms/step – loss: 0.1897 – acc: 0.9413 – val_loss: 0.0487 – val_acc: 0.9845
Epoch 2/20
60000/60000 [==============================] – 73s 1ms/step – loss: 0.0666 – acc: 0.9792 – val_loss: 0.0331 – val_acc: 0.9886
Epoch 3/20
60000/60000 [==============================] – 74s 1ms/step – loss: 0.0469 – acc: 0.9852 – val_loss: 0.0296 – val_acc: 0.9892
Epoch 4/20
60000/60000 [==============================] – 73s 1ms/step – loss: 0.0402 – acc: 0.9872 – val_loss: 0.0262 – val_acc: 0.9906
Epoch 5/20
60000/60000 [==============================] – 73s 1ms/step – loss: 0.0329 – acc: 0.9894 – val_loss: 0.0226 – val_acc: 0.9913
Epoch 6/20
60000/60000 [==============================] – 73s 1ms/step – loss: 0.0290 – acc: 0.9904 – val_loss: 0.0214 – val_acc: 0.9931
Epoch 7/20
60000/60000 [==============================] – 73s 1ms/step – loss: 0.0243 – acc: 0.9918 – val_loss: 0.0200 – val_acc: 0.9930
Epoch 8/20
60000/60000 [==============================] – 73s 1ms/step – loss: 0.0234 – acc: 0.9925 – val_loss: 0.0231 – val_acc: 0.9927
Epoch 9/20
60000/60000 [==============================] – 73s 1ms/step – loss: 0.0203 – acc: 0.9931 – val_loss: 0.0216 – val_acc: 0.9929
Epoch 10/20
60000/60000 [==============================] – 77s 1ms/step – loss: 0.0179 – acc: 0.9938 – val_loss: 0.0217 – val_acc: 0.9934Epoch 11/20
60000/60000 [==============================] – 79s 1ms/step – loss: 0.0166 – acc: 0.9945 – val_loss: 0.0233 – val_acc: 0.9925
Epoch 12/20
60000/60000 [==============================] – 78s 1ms/step – loss: 0.0167 – acc: 0.9944 – val_loss: 0.0246 – val_acc: 0.9918
Epoch 13/20
60000/60000 [==============================] – 78s 1ms/step – loss: 0.0147 – acc: 0.9953 – val_loss: 0.0194 – val_acc: 0.9941
Epoch 14/20
60000/60000 [==============================] – 78s 1ms/step – loss: 0.0124 – acc: 0.9961 – val_loss: 0.0243 – val_acc: 0.9928
Epoch 15/20
60000/60000 [==============================] – 78s 1ms/step – loss: 0.0112 – acc: 0.9960 – val_loss: 0.0217 – val_acc: 0.9934
Epoch 16/20
60000/60000 [==============================] – 78s 1ms/step – loss: 0.0133 – acc: 0.9957 – val_loss: 0.0197 – val_acc: 0.9932
Epoch 17/20
60000/60000 [==============================] – 78s 1ms/step – loss: 0.0105 – acc: 0.9963 – val_loss: 0.0214 – val_acc: 0.9939
Epoch 18/20
60000/60000 [==============================] – 78s 1ms/step – loss: 0.0109 – acc: 0.9963 – val_loss: 0.0210 – val_acc: 0.9937
Epoch 19/20
60000/60000 [==============================] – 79s 1ms/step – loss: 0.0093 – acc: 0.9968 – val_loss: 0.0218 – val_acc: 0.9938
Epoch 20/20
60000/60000 [==============================] – 79s 1ms/step – loss: 0.0109 – acc: 0.9963 – val_loss: 0.0233 – val_acc: 0.9925
Test loss: 0.02334316273004888
Test accuracy: 0.9925
Computation time:1524.597 sec
誤り率と正解率を図示するプログラムを以下に示す。
# 損失(誤り率)、正解率をグラフにする
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# 訓練データの損失(誤り率)をプロット
plt.plot(history.history['loss'],
label='training',
color='black')
# テストデータの損失(誤り率)をプロット
plt.plot(history.history['val_loss'],
label='test',
color='red')
plt.ylim(0, 1) # y軸の範囲
plt.legend() # 凡例を表示
plt.grid() # グリッド表示
plt.xlabel('epoch') # x軸ラベル
plt.ylabel('loss') # y軸ラベル
plt.show()
# 訓練データの正解率をプロット
plt.plot(history.history['acc'],
label='training',
color='black')
# テストデータの正解率をプロット
plt.plot(history.history['val_acc'],
label='test',
color='red')
plt.ylim(0.5, 1) # y軸の範囲
plt.legend() # 凡例を表示
plt.grid() # グリッド表示
plt.xlabel('epoch') # x軸ラベル
plt.ylabel('acc') # y軸ラベル
plt.show()
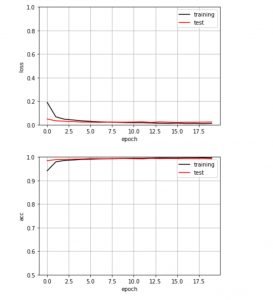
Fig.1. 上図の縦軸は誤り率、下図の縦軸は正解率
テストデータでの正解率が99.25%と過学習に陥らずに大きく向上した。CNNにプーリング層とドロップアウト層を追加挿入した成果を確認できた。
2019年12月にDeep Learningに興味を持ち、pythonで実現してみようと思い立った。夢見るディープラーニング:ニューラルネットワーク[Python実装]入門という本を図書館から借りてきて、読み始めた。最初は順調に備忘録コラムの更新ができた(2020年1月7日まで)。しかし、途中からは、この本に記載されているpythonプログラムを実行するとエラーメッセージを吐き出すばかりで、Deep Learningの学習や挙動の確認は全くできなかった。どうも、インストールしたTensorflowライブラリのバージョンが2.0.0と新しすぎるため、本に記載されているpythonプログラムが実行不能と見当がついた。そこで、python環境を少し古くし、一つ前のTensorflowのバージョン1.9.0をインストールした。この環境を実現するために、2ヶ月程の時間を要した。この作業自体は1日で完了できたので、この環境を実現する気になるのに約2ケ月程掛かったというのが正しい。いずれにしても、Tensorflowのバージョンをダウングレードすることにより、参考文献に記載されているpythonプログラムが実行可能となり、Deep Learningの基本的な考え方やNeural Networkをpythonで実現する方法を理解し、その挙動を数値実験的に追体験することができて、備忘録コラムの更新(2020年3月17日から3月22日)が出来て良かったと思う。
参考文献:
夢見るディープラーニング:ニューラルネットワーク[Python実装]入門
秀和システム、2018、金城俊哉著