局所的な2次元フィルターを用いた「畳み込みニューラルネットワーク(Convolution Neural Network: CNN)」を導入することにより、手書き数字の認識精度を更に向上させる事ができる。ニューラルネットワークの基本的構造は複数のニューロンで構成される層であり、重みによって密に結合されたこのニューロン層は全結合層と呼ばれる。全結合層は入力特徴空間の大域的パターンを学習するが、CNNの畳み込み層は空間の局所的パターンを学習し、空間における移動不変量も抽出できる。MINISTデータセットの手書き数字の分類において、全結合層が学習するパターンは全ての入力画素を含んでいるが、CNNの畳み込み層が学習するパターンは画像内のエッジ、テキスチャなど小さな2次元ウィンドウで検出されるパターンを学習する。即ち、CNNは複雑な画像の漸進的な学習と視覚概念の抽象化を学習できるので、全結合層からなるニューラルネットワークによる最大精度97%よりも更なる精度向上が期待できる。

Kerasライブラリを用いて、畳み込みニューラルネットワークを実行するプログラムを作成する。
ここでは、CNNニューラルネットワークにおける畳み込み層として10枚の異なる[3×3]の局所的2次元フィルターを設定している。畳み込み層の設定において、2Dフィルター適用時に出力画像サイズの減少回避のため、予め入力画像の周りに0値を埋め込むゼロパディング処理を仮定している。

import numpy as np
# keras.utilsからnp_utilsをインポート
from keras.utils import np_utils
# MNISTデータセットをインポート
from keras.datasets import mnist

# MNISTデータセットの読み込み
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# 訓練データ
# 60000x28x28の3次元配列を60000×28×28×1の4次元配列に変換
x_train = x_train.reshape(60000, 28, 28, 1)
x_train = x_train.astype('float32') # float32型に変換
x_train /= 255                      # 0から1.0の範囲に変換
correct = 10                        # 正解ラベルの数
# 正解ラベルを1-of-K符号化法で変換
y_train = np_utils.to_categorical(y_train, correct)

# テストデータ
# 10000x28x28の3次元配列を10000×28×28×1の4次元配列に変換
x_test = x_test.reshape(10000, 28, 28, 1)
# テストデータをfloat32(浮動小数点数)型に変換
x_test = x_test.astype('float32') # float32型に変換
x_test /= 255                     # 0から1.0の範囲に変換
# 正解ラベルを1-of-K符号化法で変換
y_test = np_utils.to_categorical(y_test, correct)

# 畳み込みニューラルネットワーク
# keras.modelsからSequentialをインポート
from keras.models import Sequential
# keras.layersからConv2D,MaxPooling2Dをインポート
from keras.layers import Conv2D, MaxPooling2D
# keras.layersからDense,Activation,Dropout,Flatten,Denseをインポート
from keras.layers import Activation, Dropout, Flatten, Dense
# keras.optimizersからAdamをインポート
from keras.optimizers import Adam
# timeモジュール
import time

model = Sequential()                 # Sequentialオブジェクトの生成
# 畳み込み層の設定
model.add(
    Conv2D(filters=10,               # フィルターの数
           kernel_size=(3, 3),       # 3×3のフィルターを使用
           padding='same',           # ゼロパディングを行う
           input_shape=(28, 28, 1),  # 入力データのサイズ 
           activation='relu'         # 活性化関数はReLU
           ))
# 出力層への入力を4次元配列から2次元に変換する
model.add(Flatten())
# 出力層の設定
model.add(Dense(10,                  # 出力層のニューロン数は10
                activation='softmax' # 活性化関数はsoftmax
               ))
# オブジェクトのコンパイル
model.compile(
    loss='categorical_crossentropy', # 損失の基準は交差エントロピー誤差
    optimizer=Adam(),                # 学習方法をAdamにする
    metrics=['accuracy'])            # 学習評価として正解率を指定

model.summary()
により、layerをまとめると以下を得る。
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 28, 28, 10) 100
_________________________________________________________________
flatten_1 (Flatten) (None, 7840) 0
_________________________________________________________________
dense_1 (Dense) (None, 10) 78410
=================================================================
Total params: 78,510
Trainable params: 78,510
Non-trainable params: 0
_________________________________________________________________

# 学習を行って結果を出力
startTime = time.time()                # プログラムの開始時刻を取得
history = model.fit(x_train,           # 訓練データ
                    y_train,           # 正解ラベル
                    epochs=20,         # 学習を繰り返す回数
                    batch_size=100,    # 勾配計算に用いるミニバッチの数
                    verbose=1,         # 学習の進捗状況を出力する
                    validation_data=(
                        x_test, y_test # テストデータの指定
                    ))
# テストデータを使って学習を評価するデータを取得
score = model.evaluate(x_test, y_test, verbose=0)
# テストデータの誤り率を出力
print('Test loss:', score[0])
# テストデータの正解率を出力
print('Test accuracy:', score[1])
# 処理にかかった時間を出力
print("Computation time:{0:.3f} sec".format(time.time() - startTime))

を実行すると、
Train on 60000 samples, validate on 10000 samples
Epoch 1/20
60000/60000 [==============================] – 10s 173us/step – loss: 0.3130 – acc: 0.9167 – val_loss: 0.1329 – val_acc: 0.9626
Epoch 2/20
60000/60000 [==============================] – 10s 161us/step – loss: 0.1158 – acc: 0.9678 – val_loss: 0.0911 – val_acc: 0.9717
Epoch 3/20
60000/60000 [==============================] – 10s 168us/step – loss: 0.0800 – acc: 0.9775 – val_loss: 0.0738 – val_acc: 0.9776
Epoch 4/20
60000/60000 [==============================] – 10s 171us/step – loss: 0.0632 – acc: 0.9819 – val_loss: 0.0676 – val_acc: 0.9782
Epoch 5/20
60000/60000 [==============================] – 10s 172us/step – loss: 0.0513 – acc: 0.9855 – val_loss: 0.0633 – val_acc: 0.9798
Epoch 6/20
60000/60000 [==============================] – 10s 173us/step – loss: 0.0439 – acc: 0.9869 – val_loss: 0.0633 – val_acc: 0.9795
Epoch 7/20
60000/60000 [==============================] – 11s 179us/step – loss: 0.0378 – acc: 0.9891 – val_loss: 0.0644 – val_acc: 0.9787
Epoch 8/20
60000/60000 [==============================] – 10s 175us/step – loss: 0.0321 – acc: 0.9909 – val_loss: 0.0617 – val_acc: 0.9793
Epoch 9/20
60000/60000 [==============================] – 11s 177us/step – loss: 0.0283 – acc: 0.9920 – val_loss: 0.0672 – val_acc: 0.9776
Epoch 10/20
60000/60000 [==============================] – 11s 183us/step – loss: 0.0247 – acc: 0.9930 – val_loss: 0.0636 – val_acc: 0.9803
Epoch 11/20
60000/60000 [==============================] – 11s 178us/step – loss: 0.0217 – acc: 0.9940 – val_loss: 0.0764 – val_acc: 0.9765
Epoch 12/20
60000/60000 [==============================] – 11s 181us/step – loss: 0.0192 – acc: 0.9948 – val_loss: 0.0676 – val_acc: 0.9788
Epoch 13/20
60000/60000 [==============================] – 11s 180us/step – loss: 0.0169 – acc: 0.9954 – val_loss: 0.0702 – val_acc: 0.9788
Epoch 14/20
60000/60000 [==============================] – 10s 171us/step – loss: 0.0151 – acc: 0.9965 – val_loss: 0.0704 – val_acc: 0.9791
Epoch 15/20
60000/60000 [==============================] – 11s 178us/step – loss: 0.0132 – acc: 0.9967 – val_loss: 0.0743 – val_acc: 0.9791
Epoch 16/20
60000/60000 [==============================] – 11s 176us/step – loss: 0.0115 – acc: 0.9974 – val_loss: 0.0736 – val_acc: 0.9804
Epoch 17/20
60000/60000 [==============================] – 11s 184us/step – loss: 0.0098 – acc: 0.9978 – val_loss: 0.0780 – val_acc: 0.9789
Epoch 18/20
60000/60000 [==============================] – 11s 182us/step – loss: 0.0092 – acc: 0.9979 – val_loss: 0.0768 – val_acc: 0.9790
Epoch 19/20
60000/60000 [==============================] – 11s 182us/step – loss: 0.0082 – acc: 0.9982 – val_loss: 0.0829 – val_acc: 0.9773
Epoch 20/20
60000/60000 [==============================] – 11s 182us/step – loss: 0.0072 – acc: 0.9987 – val_loss: 0.0808 – val_acc: 0.9796
Test loss: 0.08083874053675973
Test accuracy: 0.9796
Computation time:212.996 sec

畳み込みニューラルネットワーク(CNN)による正解率は学習回数(epock)を4回繰り返すとほぼ98%に向上するが、学習回数を20回に増加してもテストデータの正解率は98%が上限と判断できる。

以下のプログラムを実行して誤り率と正解率をグラフにする。

# 損失（誤り率）、正解率をグラフにする
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 訓練データの損失(誤り率)をプロット
plt.plot(history.history['loss'],
         label='training',
         color='black')
# テストデータの損失(誤り率)をプロット
plt.plot(history.history['val_loss'],
         label='test',
         color='red')
plt.ylim(0, 1)       # y軸の範囲
plt.legend()         # 凡例を表示
plt.grid()           # グリッド表示
plt.xlabel('epoch')  # x軸ラベル
plt.ylabel('loss')   # y軸ラベル
plt.show()

# 訓練データの正解率をプロット
plt.plot(history.history['acc'],
         label='training',
         color='black')
# テストデータの正解率をプロット
plt.plot(history.history['val_acc'],
         label='test',
         color='red')
plt.ylim(0.5, 1)     # y軸の範囲
plt.legend()         # 凡例を表示
plt.grid()           # グリッド表示
plt.xlabel('epoch')  # x軸ラベル
plt.ylabel('acc')    # y軸ラベル
plt.show()

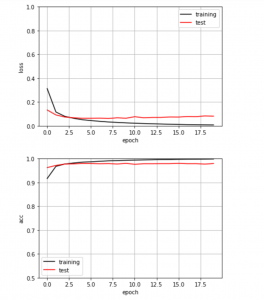
Fig.1. 上図の縦軸は誤り率、下図の縦軸は正解率を表し、両図とも横軸はepochである。