機械学習のためのTensorflowライブラリをより簡単なコードで動かすためにKerasライブラリがある。Kerasはpythonでディープラーニングを行うためのフレームワークであり、色々な種類のディープラーニングモデルを用いて訓練・学習を実施する便利な手段を提供する。F. Cholletが2015にKerasをディープラーニングの実検を素早く実施できる様に、研究者向けに開発したものである。しかし、KerasはユーザーフレンドリなAPI(Application Programming Interface)を備えているため、現在では研究者のみならず、エンジニアから学生まで人気の高いディープラーニング用フレームワークとなっている。ここでは、Kerasライブラリでどの様にニューラルネットワークを構築し、どの様に学習をするのかを述べる。

(1) MNISTデータセットの読み込みと加工をするプログラム例を示す。

import numpy as np
# keras.utilsからnp_utilsをインポート
from keras.utils import np_utils
# MNISTデータセットをインポート
from keras.datasets import mnist

# MNISTデータセットの読み込み
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# 訓練データ
# 60000x28x28の3次元配列を60000×784の2次元配列に変換
x_train = x_train.reshape(60000, 784)
# 訓練データをfloat32(浮動小数点数)型に変換
x_train = x_train.astype('float32')
# データを255で割って0から1.0の範囲に変換
x_train = x_train / 255
# 正解ラベルの数
correct = 10
# 正解ラベルを1-of-K符号化法で変換
y_train = np_utils.to_categorical(y_train, correct)
# テストデータ
# 10000x28x28の3次元配列を10000×784の2次元配列に変換
x_test = x_test.reshape(10000, 784)
# テストデータをfloat32(浮動小数点数)型に変換
x_test = x_test.astype('float32')
# データを255で割って0から1.0の範囲に変換
x_test = x_test / 255
# 正解ラベルを1-of-K符号化法で変換
y_test = np_utils.to_categorical(y_test, correct)

これを実行すると、
Using TensorFlow backend.
というメッセージが返ってくる。
上記のプログラム内の19行目のコメント文で#正解ラベルを1-of-K符号化法で変換と記述したが、Kerasのnp_utils.to_categorical()　関数の第2引数として正解ラベル数としてcorrect = 10を指定したので、正解ラベルが3 の場合は、4番目の要素のみが1になる要素数10の[0., 0., 0., 1., 0., 0., 0., 0., 0., 0.] 配列に変換することを意味する。これを2階テンソル化した行列を y_train に戻す。即ち、print(y_test)を実行すると以下に示す様な10個の要素からなる配列を10,000個が出力される。
[[0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
[0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
………..
[0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]]

Kerasによるニューラルネットワークの実装は簡単である。
(1) まず、Sequential()コンストラクターでニューラルネットワークの基本となるSequentialクラスのオブジェクトを生成し、各層の設定を行い、オブジェクトに登録する。ここでは、ます、入力層のニューロン数を784、ニューロン数200、活性化関数はReLUで構成される隠れ層を定義し、add()メソッドでSequentialオブジェクトに登録する。

Dense()は層を表現するDenseオブジェクトを生成するコンストラクターであり、

Dense(ニューロン数、input_dim = 入力されるニューロン数、activation = ‘活性化関数’ )で定義される。

(2)次に、ニューロン数10, sigmoid()関数を活性化関数とする出力層を登録する。
(3)最後に、compile()メソッドでSequentialオブジェクトをコンパイルする。この時、パラメータとして学習に使用する方法や誤差の測定法などを指定する。

# ニューラルネットワークの構築
# keras.modelsからSequentialをインポート
from keras.models import Sequential
# keras.layersからDense、Activationをインポート
from keras.layers import Dense, Activation
# keras.optimizersからAdamをインポート
from keras.optimizers import Adam

model = Sequential()                 # Sequentialオブジェクトの生成
model.add(Dense(200,                 # 隠れ層のニューロン数は200
                input_dim=784,       # 入力層のニューロン数は784
                activation='relu'    # 活性化関数はReLU
               ))
model.add(Dense(10,                  # 出力層のニューロン数は10
                activation='sigmoid' # 活性化関数はsigmoid
               ))
model.compile(                       # オブジェクトのコンパイル
    loss='categorical_crossentropy', # 損失の基準は交差エントロピー誤差
    optimizer=Adam(),                # 学習方法をAdamにする
    metrics=['accuracy']             # 学習評価として正解率を指定
    )

model.summary() を出力すると、以下を得る。
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 200) 157000
_________________________________________________________________
dense_2 (Dense) (None, 10) 2010
=================================================================
Total params: 159,010
Trainable params: 159,010
Non-trainable params: 0
_________________________________________________________________

ここでは誤差の基準で、確率を出力するモデルを扱う時は交差エントロピーの使用が最適とされているのでそれを指定した。また、学習方法として従来の勾配法は「局所解」に陥る欠点があり、これを改良する確率的勾配法が提案されたが、ここでは確率的勾配法を更に改良したAdam(Adaptic moment estimation)手法を指定する。

# 学習を行って結果を出力
import time

startTime = time.time()
history = model.fit(x_train,           # 訓練データ
                    y_train,           # 正解ラベル
                    epochs=5,          # 学習を繰り返す回数
                    batch_size=100,    # 勾配計算に用いるサンプル数
                    verbose=1,         # 学習の進捗状況を出力する
                    validation_data=(
                        x_test, y_test # テストデータの指定
                    ))
# テストデータで学習を評価するデータを取得
score = model.evaluate(x_test, y_test, verbose=0)
# テストデータの誤り率を出力
print('Test loss:', score[0])
# テストデータの正解率を出力
print('Test accuracy:', score[1])
# 処理にかかった時間を出力
print("Time:{0:.3f} sec".format(time.time() - startTime))

Train on 60000 samples, validate on 10000 samples
Epoch 1/5
60000/60000 [==============================] – 4s 73us/step – loss: 0.3234 – acc: 0.9124 – val_loss: 0.1638 – val_acc: 0.9534
Epoch 2/5
60000/60000 [==============================] – 4s 61us/step – loss: 0.1384 – acc: 0.9604 – val_loss: 0.1186 – val_acc: 0.9641
Epoch 3/5
60000/60000 [==============================] – 4s 61us/step – loss: 0.0959 – acc: 0.9724 – val_loss: 0.0876 – val_acc: 0.9735
Epoch 4/5
60000/60000 [==============================] – 4s 62us/step – loss: 0.0730 – acc: 0.9784 – val_loss: 0.0853 – val_acc: 0.9736
Epoch 5/5
60000/60000 [==============================] – 4s 62us/step – loss: 0.0580 – acc: 0.9832 – val_loss: 0.0750 – val_acc: 0.9761
Test loss: 0.07500464550508186
Test accuracy: 0.9761
Time:19.757 sec

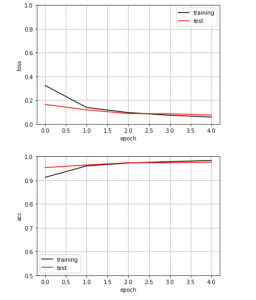
誤り率と正解率をグラフにするkeras_nn.py

# 損失（誤り率）、正解率をグラフにする
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 訓練データの損失(誤り率)をプロット
plt.plot(history.history['loss'],
         label='training',
         color='black')
# テストデータの損失(誤り率)をプロット
plt.plot(history.history['val_loss'],
         label='test',
         color='red')
plt.ylim(0, 1)       # y軸の範囲
plt.legend()         # 凡例を表示
plt.grid()           # グリッド表示
plt.xlabel('epoch')  # x軸ラベル
plt.ylabel('loss')   # y軸ラベル
plt.show()

# 訓練データの正解率をプロット
plt.plot(history.history['acc'],
         label='training',
         color='black')
# テストデータの正解率をプロット
plt.plot(history.history['val_acc'],
         label='test',
         color='red')
plt.ylim(0.5, 1)     # y軸の範囲
plt.legend()         # 凡例を表示
plt.grid()           # グリッド表示
plt.xlabel('epoch')  # x軸ラベル
plt.ylabel('acc')    # y軸ラベル
plt.show()

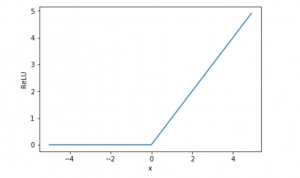
隠れ層の活性化関数として用いたReLU()関数はRectified Linear Unit(正規化線形関数)の略で、最善の活性化関数であるとされている。Sigmoid関数は入力値がある程度大きくなると常に1に近い値をとり、勾配法による学習が遅くなる欠点があるが、ReLU関数は入力値が0以下では0となり、入力値が0より大きい時は入力値をそのまま出力するので、学習の停滞を回避できるメリットがあるとされている。

ReLU関数のグラフは以下のプログラムで表示できる。

import numpy as np
import matplotlib.pylab as plt
%matplotlib inline

def relu(x):
    # maximum()は2つの配列を比較して大きい要素を返す
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.show()

この投稿で提示したように、ラルネットワークを用いた学習による手書き数字の認識の精度は大体97%になることが確認できた。